
Breeding Systems



In the real world, populations rarely mate at random for a number of reasons:
Examples of non-random mating are wide-spread. (Graham Bell's "The Masterpiece of Nature" is an excellent source of examples.)
Today we will examine a number of systems of non-random mating and explore their impact on the dynamics of a population.


If two alleles within a diploid individual are identical by descent (that is, both alleles are direct descendants of a single allele in an ancestor), such alleles are called autozygous.
If the alleles are not identical by descent (as far as is known), they are called allozygous.
The inbreeding coefficient (F) measures the probability that two alleles are identical by descent (autozygous).


where FI is the inbreeding coefficient of the individual in question, the sum is over all distinct paths through each of the common ancestors, i is the number of individuals in a loop up to a common ancestor and back (counting the common ancestor but not counting the individual in question), and FA is the inbreeding coefficient of a common ancestor.
Worked Examples.


Consider two alleles (A1,A2) at a single locus.
Remember: F (the inbreeding coefficient) is the probability that an individual's alleles are identical by descent = autozygous (A1A1 or A2A2).
Choose an allele from the population at random and say it is A1 (with probability p). With probability F the other allele is autozygous (must be A1), while with probability 1-F it is allozygous (drawn at random: A1 with probability p and A2 with probability q).
Therefore the total probability that an individual is A1A1 is p (F+(1-F)p) = p2 (1-F) + p F.

Therefore, F measures the extent to which the oberved proportion of heterozygotes (H) departs from the expectation of 2pq: F = (2pq-H)/2pq. In practise, this is often how F is determined.
Notice: The allele frequency of A1 within the inbred population is still p!


At equilibrium, F[t]=F[t-1], so that F*=1/2(1+F*). The only equilibrium solution to this is F*=1. How fast does F approach its equilibrium value of 1?
It is convenient to measure the departure of F[t] from its equilibrium value of 1. From above, 1-F[t]=1/2 (1-F[t-1]), which can be easily iterated.
If the parent was itself produced by selfing, then 1-F[t-1]=1/2 (1-F[t-2]) giving 1-F[t]=(1/2)2 (1-F[t-2]).
After t generations of selfing, we obtain

 Heterozygosity halves every generation and the inbreeding coefficient rises rapidly to one.
Heterozygosity halves every generation and the inbreeding coefficient rises rapidly to one.


The equilibrium now solves F*=1/2 (1+F*) S, which leads to an equilibrium inbreeding level of S/(2-S).
Again, it is easier to iterate the departure of F[t] from its equilibrium value:

 Every generation the departure from equilibrium is reduced by the proportion S/2.
Every generation the departure from equilibrium is reduced by the proportion S/2.
The population approaches the equilibrium inbreeding level of S/(2-S). This approach to equilibrium is rapid when the selfing rate is high (getting nearly half-way there every generation) and even faster when the selfing rate is low (but the population doesn't have far to go in this case).


The strength of inbreeding can be measured by the proportion, 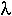 , by which heterozygosity decreases every generation.
, by which heterozygosity decreases every generation.
For example,
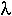 = 0.5
= 0.5
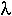 = 0.809
= 0.809
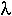 = 0.920
= 0.920
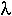 = 0.927
= 0.927


Remember: At mutation-selection balance in the diploid model, the frequency of mutants, A2, is 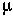 /hs and the mean fitness of the population is 1-2
/hs and the mean fitness of the population is 1-2 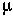 .
.
What happens when a randomly mating population at a mutation-selection balance is inbred? (Assume that inbreeding occurs for only one generation leading to an inbreeding coefficient of F.)

 Recessive mutant frequency rises
Recessive mutant frequency rises

 Mean fitness declines when h < 1/2
Mean fitness declines when h < 1/2
This phenomenon of mean fitness declining with inbreeding is known as inbreeding depression.


We now need to recalculate the recursions and the equilibrium.
The recursions are derived as before, with

although now the adult frequencies reflect the fact that the population was created by inbreeding:

These equations can again be analysed (See Mathematica sheet).
 With regular inbreeding, the frequency of mutations declines and the mean fitness increases.
With regular inbreeding, the frequency of mutations declines and the mean fitness increases.
This phenomenon, whereby mutations are more efficiently eliminated from a population that is inbred, is known as purging.


Negative Assortative Mating is the propensity to mate with phenotypically different individuals.
Consider positive assortative mating occurring at rate m.
If assortment is on the basis of gamete genotype, with A1 gametes preferring to unite with A1 gametes over all others, the dynamics at a single locus are equivalent to those under inbreeding.

The only difference would be that inbreeding affects all loci equally whereas assortative mating acts primarily on the A locus (although linked loci would also exhibit decreased heterozygosity).
The effects of assortative mating are more complex when assortment is based on the diploid parents' genotypes. Now, one has to specify whether all genotypes are phenotypically distinct and whether there is dominance. Furthermore, one has to specify whether assortment occurs via female preferences for similar males (a form of sexual selection) or whether assortment occurs because individuals form groups, within which mating is random.
As an example, we will construct a mating table for the case where the A1 allele is completely dominant and causes its carriers to prefer a different site (e.g., host plant) than A2A2 individuals and where m the probability that mating occurs within the group.


An example is gametophytic self-incompatibility in plants (eg Brassica), where the pollen must carry an allele different than either of the two alleles carried by the female diploid plant in order to fertilize an ovule.
Self-incompatibility requires a minimum of three alleles (A1,A2,A3), each of which is always found in heterozygous condition. A1 pollen, for example, can only fertilize an egg of an A2A3 individual.
A new allele (A4) that arises in this population will have a selective advantage, however, since A4 pollen can fertilize all of the other individuals in the population.
In contrast to inbreeding and positive assortative mating within groups, negative assortative mating tends to cause alleles to change in frequency, with rare alleles finding more mates and rising in frequency.