An excellent introductory text is The Evolution of Life Histories (1992) by Stephen Stearns, which should be consulted for more detailed information and examples.

Web sites of interest are:

• Browse a rich source of information on aging
• Find out how long you'll live!!

Life Tables Consider a population measured at particular points in time (eg every year after the breeding season).

We start by discussing the dynamics of a single genotype with constant life history parameters. For simplicity we count only females.

Demographic parameters of the population include:

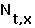• the number of females at time t in age class X
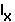• the probability of surviving from birth to the beginning of age class X
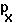• the probability of surviving from age class X to age class X+1
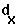• the probability of dying from age class X to age class X+1
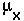• the instantaneous death rate at age X
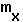• the number of offspring per female in age class X

Relations between the variables:

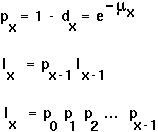
The average lifetime reproductive success is:

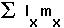
Given the population composition at time t, at time t+1:

(1) the number of newborns is

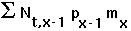
(2) the number of individuals in other age classes is simply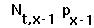

Population changes can more easily be described using matrix notation:

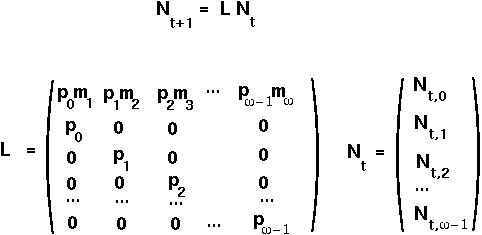
L is known as a Leslie Matrix for population projection.

RESULT: The distribution of the population across age classes rapidly reaches a stable age distribution at which point the number of individuals in each age class grows exponentially at rate r.

EULER-LOTKA EQUATION To determine r, note that the total number of newborn individuals can be related to the total number of newborns at all previous times:

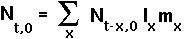
If each age class were growing exponentially at rate r then

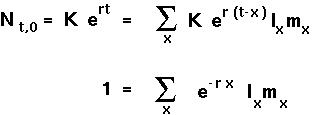
This is the Euler-Lotka equation and it can be solved for r, given the life history table of a population.

NOTE: The largest eigenvalue of the Leslie Matrix, 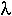, is equal to 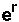. This is an alternate way to find r, although it is algebraically the same.

Hamilton (1966) (see also Charlesworth 1980) showed that the selection pressures acting on life history are best measured by the sensitivity of r to changes in fecundity or instantaneous survival rate:

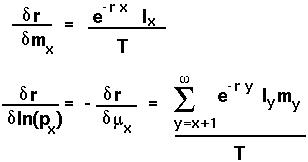
That is, changes in the 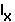or 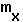only matter in so much as these changes are reflected in r.

Alleles that influence life history such that r is increased spread at a faster rate than other alleles and invade the popuation.

Notice that the sensitivities always decrease with increasing X, which happens because alleles that act late in life have a lower chance of ever being expressed due to mortality in previous age classes.

Alleles acting late in life experience affect r less strongly and thus experience a weaker selective pressure than alleles acting early in life.

This has three evolutionary consequences:

• (1) Alleles that increase early survival or fertility at the cost of late survival or fertility tend to be favored.
• (2) Deleterious alleles that decrease early survival or fertility will be more strongly selected against than alleles that decrease late survival or fertility.
• (3) Beneficial alleles that increase early survival or fertility will be more strongly favored than alleles that increase late survival or fertility.

This is the evolutionary explanation for senescence

"defined as the tendency for the age-specific survival probabilities and fecundities to decline with age, for individuals of sufficiently advanced age. This process of decline at the level of life-history traits reflects the decline in performance of many different physiological functions with respect to age, and the increase in incidence of pathological factors such as cancer and cardio-vascular disease."

It remains to be determined experimentally which of the three explanations above is the most relevant cause of senescence in natural populations:

• (1) Antagonistic pleiotropy (or optimized life history or "disposable soma")
• (2) Deleterious mutation pressure
• (3) Reduced adaptability of late age classes (lag-load)

There are multiple mechanisms by which senescence can occur, most of which center around the hypothesis that repair is never complete and therefore damages accumulate.

It may be selectively advantageous for higher organisms to adopt an energy saving strategy of reduced accuracy in somatic cells to accelerate development and reproduction, but the consequence will be eventual deterioration and death. This 'disposable soma' theory of the evolution of ageing also proposes that a high level of accuracy is maintained in immortal germ line cells, or alternatively, that any defective germ cells are eliminated.

More than 2% of a cell's energy budget is spent on checking and correcting DNA and proteins within the cell (Stearns 1992, p. 201).

The "disposable soma" hypothesis is that organisms reduce the energy spent on repair in order to devote resources to early survival and reproduction, to the detriment of late survival and reproduction.