"As a result of complex biochemical, developmental, and regulatory pathways, a single gene will almost always influence multiple traits, a phenomenon known as pleiotropy (Wright 1968)."

- Lynch and Walsh (1998)

"In most population genetic models, alleles at a gene locus enter a model only through their frequencies in a population and through their contribution to an individual's fitness...However, molecular biology has demonstrated that genes and their products have a complex substructure that most population genetic modeling has not yet captured."

- Wagner (1998)

What can we say about the magnitude of pleiotropic effects that occur as alleles rise in frequency through selection for a specific trait?

Example

The evolution of corn

Approximately five major regions of the genome are responsible for the morphological transition from a teosinte-like ancestor to modern corn.

Two of these regions have been identified recently by John Doebley et al. (1995), who noted that "each affect a number of different aspects of plant morphology."

For example, one QTL maps to a gene (teosinte branched 1) that had a significant effect on all nine traits measured:

• Length of internodes in the ear
• Number of fruitcases in a row on the ear
• Tendency of ear to shatter
• % of fruitcases with single vs. two kernels
• % lateral branches with male tassels
• Degree to which the fruitcases are stacked vs. side-by-side
• Number of internodes in the lateral branches
• Average length of these internodes
• Number of branches in the primary lateral inflorescence

Known maize mutants at tb1 have similar pleiotropic effects.

Scenario: Consider a trait subject to direct artificial or natural selection.

Notation: An allele that positively affects the trait under selection will experience a direct selective advantage (s_d) as well as pleiotropic selection (s_p).

Claim: Just as most mutations that affect fitness are deleterious, we would expect the total pleiotropic effects of an allele to negatively affect fitness (s_p < 0).

But what distribution will s_p follow?

Can we say anything about the extent of pleiotropy expected among favorable alleles?

The uniform distribution offers a clue!!

An allele will only be favorable overall if s_T = s_d + s_p is positive.

But the mean value of s_p within the range where s_T > 0 is simply -s_d/2, which does not depend on the unknown mean of the distribution!!

Claim: For many distributions of s_p, the average amount of pleiotropy seen among favorable alleles will be roughly -s_d/2 as long as the mean magnitude of pleiotropy (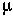) is large relative to the strength of direct selection.

e.g. Exponential distribution of pleiotropic effects:

Note 1: The only distributions for which this approximation does not work are those that fall or rise rapidly, e.g. the gamma distribution with a high coeffecient of variation (C).

For the gamma distribution, the average amount of pleiotropy seen among favorable alleles is roughly -s_d/(1+C^2) as long as 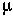> s_d.

Note 2: If new mutations are the source of genetic variation, not only must s_T be positive, but also the mutations must fix, which is more probable for larger values of s_T.

Among fixable mutations, the average pleiotropic effect on fitness is -s_d/3.

Implications

"The available evidence indicates that pleiotropy is virtually universal."

- Wright (1968)

This work provides a null expectation for the effect on fitness of pleiotropy.

If pleiotropy is extensive, it should roughly halve the total strength of selection for alleles that spread within a population in response to selection.

It may be hard to identify, in hindsight, the exact traits that have been favored by natural selection, since a suite of phenotypic changes, even costly ones, may have arisen pleiotropically.

Prediction:In an artificial selection experiment, the population should return towards the original mean after artificial selection has ceased at a rate that is approximately half the original rate of response.

This assumes that selection is weak enough that little hitchhiking occurs. Otherwise, hitchhiking and pleiotropy will work together to reduce the average rate of response to selection.