Biology 303 sec.102, Sept.-Dec. 2004; Some Thoughts on R₀ and r.

Generally, a population grows as (Krebs, p.140):

where: e is a constant (approx. 2.71828, the base of natural logarithms)

N is population density

t is time (0 at the start, and t some time-period “t” later)

r is the intrinsic rate of population increase under prevailing conditions

If you wish to know how quickly a population grows per generation, use G (generation time):

(this is given as “T” instead of “G” in Krebs’ notation)

Take the natural log of this equation, rearrange it, and you get:

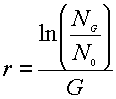
The value in the brackets is essentially the multiplier by which population size has changed in one generation, or the relative change in number of breeders per generation. We also call this term the population net reproductive rate, and symbolize it as R₀.

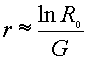
[This value can also be derived from life-table data; see downloadable Demography document.]

This gives only the approximate value for r, since it assumes non-overlapping generations.

The theoretically ideal value for r – a population’s theoretic intrinsic maximum capacity for growth – can never be realized by organisms in the real world. An exponentially growing population in a laboratory container may approach the theoretical maximum, or r_max, early in its growth, but never be actually “at” it, because as soon as some individuals are present in an environment that place can no longer support idealized growth – food has been depleted, waste-products are present, etc., it’s no longer a “perfect” growth medium. A population will exhibit a realized situation-specific value of r, called r_a or r_obs (“actual”, or “observed”, r), which varies from a little less than r_max, through positive values (increasing population), and zero (stable population size), to negative values (declining population size). See Box 11.1, page 162, in Krebs for a different explanation of this point. The units of r are individual/individual/time, and it’s an instantaneous rate, saying how the population is changing “right now”.

The instantaneous value of r is the difference between the per-individual birth rate and the per-individual death rate at that given instant in time:

How can rates be “per individual”? For births, you can imagine the number of offspring produced per female per season, or in a population in which not all females breed every season you could have the fraction of total females present which produced an offspring per season. Either of these is in units of individual/individual/time.

For deaths, the easiest way to picture it is the number of individuals dying out of the total number of individuals present during a time-period, or equivalently the fraction dying per time period. This sort of measure will also be in units of individual/individual/time.

If you want a finite rate (a prediction of what will happen a finite period into the future), use the calculation of l (lambda):

Krebs offers an example of this difference in usage at the end of Box 10.2, p.145, but you will not be asked to use this calculation.