Study Questions for Final

In the logistic model, when do you expect population growth to be nearly exponential?

Present a proof of your answer.

Microsatellites are short, repeated sequences within the genome, eg CACACACACA is a CA repeat that is 5 repeats long.

Microsatellites tends to have a relatively high mutation rate, with mutations frequently involving a gain or a loss of a single repeat during DNA replication. This is thought to occur due to slippage of the DNA as the DNA replication machinery passes over the microsatellite.

The probability of slippage is assumed to increase with the number of repeats, n[t], in the microsatellite at time t.

Part 1:

Let n[t] be the probability that the microsatellite increases by one repeat in a generation.

Let n[t] be the probability that the microsatellite decreases by one repeat in a generation.

Write down an equation for the expected value of n[t+1] as a function of n[t]. Simplify your result and answer the following questions:

Which model of population growth does this equation correspond to?
What does that tell you about how the number of repeats in a microsatellite will change over time?
What condition must hold for the number of repeats to remain constant over time?

Part 2:

Assume instead that deletions become more common as the length of the microsatellite increases (perhaps loops form more readily during DNA replication causing more deletions). Let the probability that the microsatellite decreases by one repeat in a generation now equal n[t]².

Write down the expected value of n[t+1] as a function of n[t]. Simplify your result and answer the following questions:

Which model of population growth does this equation correspond to? (Relate the variables in each model to one another.)
What does that tell you about how the number of repeats in a microsatellite will change over time?
When will the number of repeats remain constant over time?

[NOTE: Throughout this question, assume that and are very small positive quantities such that n[t] and n[t]² are always less than one.]

In the haploid selection model, say that the fitness of allele a is 1 and the fitness of allele A is (1+s).

Write down the recursion equation for the frequency of A at time t+1 as a function of its frequency at time t (use p[t] for the frequency of A).

What is the change in frequency of allele A from one generation to the next (ie find p)?

Perform a Taylor Series on p with respect to s and, assuming that selection is weak, ignore s² and higher terms. By this method, show that p = s p (1-p) + O(s²)

[Hint: This is a somewhat different use of the Taylor Series than what we've done before. Remember that the Taylor Series says that a function f(x) can be written as f(a) + x f'(a) + x² f''(a)/2 + ... Now, we say that p is a function of selection, f(s), and we write f(s) = f(0) + s f'(0) + s² f''(0)/2 + ... Dropping s² and higher order terms, we get that f(s) is approximately f(0) + s f'(0) when s is small, where f(0) is p when s equals 0 and f'(0) is the derivative of p evaluated at the point s=0.]

Using the fact that p is approximately s p (1-p), when will the gene frequency change at the fastest rate?

[Hint: To find a maximum or a minimum of a function, take the derivative of the function with respect to the variable of interest and set this derivative to zero. Then solve the equation for the variable of interest.]

Several other functions besides the logistic equation have been used to describe density dependent growth. One such function is the Gompertz differential equation:

dn/dt = -

n ln(n/K).

Population size tends to increase more rapidly at low population sizes under the Gompertz equation than under the logistic equation.

This point is illustrated in the following graph with n[0]=1, K=100, and =0.1. Here, r for the logistic equation was chosen to have the same expected time until 50 individuals were present in the population (19 generations).

What are the equilibria of the Gompertz equation?

When is the equilibrium (with the species present) locally stable?

Challenge: A global solution to the Gompertz equation can be found by making a substitution of variables from n to y, using y=ln(n/K). First, what is n in terms of y? Second, what is dn/dt in terms of dy/dt (you will need to use the chain rule)? Make these substitutions into the Gompertz equation, simplify, and integrate the resulting equation to obtain the general solution for the population size at all future times.

In this problem, we will look at the degree of somatic mosaicism that is expected to occur in a multicellular organism.

Consider the genotype of the developing individual. When the zygote is first formed, it has its original genotype (call this the non-mutant). Every cell division, there is a chance 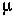that a mutation will occur. Ignore back-mutations.

Write down the frequency of non-mutant and mutant cells as a function of the number of cell divisions since zygote formation, t.

In an organism that undergoes 100 cell divisions during development, what fraction of the cells will be mutant at a particular gene at the end of development if 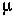equals 10^-7 per cell division?

Across an entire genome of 10⁵ genes, 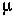would be approximately 10^-2 per cell division. What fraction of cells in the adult will carry a mutant gene somewhere in the genome?

You have been contacted to figure out the effect of removing red squirrels on the age distribution of a population of snowshoe hares.

Assume that snowshoe hares live for a maximum of two years (consider only two age classes).

Census in the summer immediately after the breeding season. Newborn individuals survive predation with a 25% probability and survive starvation over winter with a 50% probability. Let's assume that older individuals aren't at risk of predation, but that one year old individuals still have a 50% probability of dying over winter. Individuals that are two or older never survive winter.

If the newborns survive to the next year, they will have four babies in the following spring. If the one year olds survive to the next year, they will have eight babies.

If red squirrels are removed, predation among the newborns declines, and the probability of surviving predation goes up to 75%. What effect would red squirrel removal have on the growth rate of the population and its age distribution?

You are presented with a series of linear equations that you solve by matrix manipulation. In your general solution, you let time go to infinity and find that the system reaches a specific point.

Is this point an equilibrium?

Is it unstable or stable? If stable, is it locally or globally stable? Should you do a local stability analysis?

Which of the following sets of equations is non-linear?

(a)

n₁[t+1] = a n₁[t] + b n₂[t]

n₂[t+1] = c n₁[t] / n₂[t]

(b) n₁[t+1] = a n₁[t] + b n₂[t] - c n₂[t]

n₂[t+1] = d n₁[t] + e n₂[t] - f n₂[t]

n₂[t+1] = b n₁[t]

(d) n₁[t+1] = a n₁[t] + b n₁[t] n₂[t]

n₂[t+1] = c n₂[t] + d n₁[t] n₂[t]

(e) n₁[t+1] = a n₁[t]²

n₂[t+1] = b n₁[t] + c n₂[t]

Describe in words how you would analyse the linear sets of equations and the non-linear sets of equations to get a sense of how the dynamical systems behave.

In this question, you will analyse a source-sink model.

Consider two populations of a single species, one in a good environment (population 1) and one in a poor environment (population 2). The number of individuals in the two populations is n₁ and n₂, respectively.

In the good environment, the population is able to grow logistically with a carrying capacity, K₁, and an intrinsic rate of growth, r₁. Each generation, a proportion, m, migrate to the poor environment (this is the "source" population).

In the poor environment, each individual has R offspring. R is less than one and the population is unable to replace itself (this is the "sink" population). The sink population is maintained by the constant input of migrants every generation from the source population.

Equations describing this model are:

n₁[t+1] = n₁[t] (1-m) + n₁[t] r₁ (1-n₁[t]/K₁)

n₂[t+1] = R n₂[t] + m n₁[t]

What are the equilibrium population sizes for the two populations in this model?

Under what conditions is the source-sink metapopulation stable?

An alternative formulation of the equations for competition among two species is as follows (from Renshaw 1991):

n₁[t+1] = a₁ n₁[t] / (1 + b₁ n₁[t] + c₁ n₂[t])

n₂[t+1] = a₂ n₂[t] / (1 + b₂ n₂[t] + c₂ n₁[t])

a_i is a measure of the growth rate of population i (equivalent to 1+r_i), b_i is a measure of the effects of intraspecific competition on growth rate, and c_i is a measure of the effects of interspecific competition on growth rate.

(a) Identify all the equilibrium states of the population.

(b) Three of these equilibria lack one or both species. Determine the conditions under which each of these three equilibria are stable.

(c) Gause (1932) studied competition in yeast (Saccharomyces cerevisiae and Schizosaccharomyces pombe) and estimated the following parameters: a₁ = 1.2439, a₂ = 1.0626, b₁ = 0.0188, b₁ = 0.0173, c₁ = 0.0591, c₂ = 0.0047. Using these numbers, determine whether any of the three equilibria studied in (b) is stable. If any equilibrium is stable, explain why the absent species does not spread in terms of the parameters of the model.

For the following word problems, answer the question and say which probability distribution describes the problem.

(a) Say that there is a 5% error rate in each experiment that a scientist does (ie that 5% of the time the scientist will think that they have a significant result when they don't or vice versa). On average, how many experiments will a scientist do before reaching their first false conclusion?

(b) You are tracking rabbits and observe one rabbit every 1.5 hours, on average. What is the probability that the first rabbit you see is in the last hour of an 8 hour day?

(c) You are trying to sequence a 500 basepair region of DNA, but you know that your method introduces sequencing errors at a rate of 0.001/basepair. What is the probability of obtaining the correct sequence entirely? What is the probability of getting exactly one error? What is the probability of getting more than one error?

(d) You are watching salmon swim by in a river and have, in the recent past, seen about one fish every ten minutes. You decide to wait for 10 fish to pass before heading home. How long do you expect to wait? What will the standard deviation of this estimate be? Since you realise that this is the sum of several independent events occurring, you decide it is reasonable to approximate the distribution using a normal distribution. From your statistics class, you remember that 95% of a normal distribution lies within 2 standard deviations of the mean. What is the 95% confidence interval in this case?

For each of the following distributions, describe the possible values that a random variable can take? (That is, specify the domain of the distribution using words like "the integers from 0 to infinity".)

(a) Binomial distribution

(b) Exponential distribution

(d) Normal distribution

(e) Geometric distribution

(f) Gamma distribution

When will the geometric distribution (discrete) and the exponential distribution (continuous) have similar means and variances? Explain why your answer makes sense.

[Hint: The distinction between the two distributions is vaguely analogous to whether you compound interest yearly or continuously.]

Show that the mean of an exponential distribution is 1/

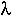[Hint: Integrate by parts to solve this integral:

]