When the population size is very far below the carrying capacity.

Proof 1: The logistic equation in discrete time is:

n[t+1] = n[t] + r n[t] (1-n[t]/K)

If n[t] is very small relative to K, then (1-n[t]/K) will be nearly 1. Then the equation becomes:

n[t+1] ~ n[t] + r n[t],

which is the equation describing exponential growth in discrete time (n[t+1] = R n[t], where R = 1+r).

Proof 2: The logistic equation in continuous time is:

dn/dt = r n (1-n/K)

If n is very small relative to K, then (1-n/K) will be nearly 1. Then the equation becomes:

dn/dt = r n

which is the equation describing exponential growth in continuous time (dn/dt = r n).

If n[t] is the probability that the microsatellite increases by one repeat in a generation and n[t] is the probability that the microsatellite decreases by one repeat in a generation, then

n[t+1] = n[t] + 1* n[t] - 1* n[t]

n[t+1] = n[t] (1+ - )

This is analogous to the model of exponential growth, with R = (1+ - ).

This tells us that the number of repeats will

• increase exponentially if (1+ - ) > 1, ie >
• decrease exponentially if (1+ - ) < 1, ie <
• remain constant if (1+ - ) =1.

Part 2:

If n[t] is the probability that the microsatellite increases by one repeat in a generation and n[t]² is the probability that the microsatellite decreases by one repeat in a generation, then

n[t+1] = n[t] + 1* n[t] - 1* n[t]²

n[t+1] = n[t] (1+ - n[t])

This is analogous to the model of logistic growth [n[t+1] = n[t] + r n[t] (1-n[t]/K)] in discrete time, with r = and K = /.

This tells us that the number of repeats will increase towards a "carrying capacity" if is positive.

The number of repeats will remain constant (at equilibrium) when n[t] = /, assuming that is positive.

Notice that there will only be more than one repeat at equilibrium if >

The change in allele frequency over one generation is:

p = p[t+1] - p[t] = (1+s) p / (1 + s p) - p = (p + s p - p - s p²) / (1 + s p)

= s p (1-p) / (1 + s p)

If we call p f(s), note that:

Putting these terms in the Taylor Series gives: f(s) = f(0) + s f'(0) = s p (1-p). Therefore, if s is small, p is approximately s p (1-p).

The maximum rate of change will occur at p=1/2. We can tell that a maximum or a minimum must occur at p=1/2 since at this point, d(p)/dp=0. We can tell it is a maximum since the double derivative of p with respect to p is negative (which implies a concave function).

To perform a stability analysis, we first need to find the derivative of the differential equation with respect to n.

d(- n ln(n/K))/dn = - ln(n/K) - n * 1/n

[Remember that d(ln(n))/dn = 1/n and d(ln(n/K))/dn = 1/(n/K) * d(n/K)/dn = 1/(n/K) * 1/K = 1/n.]

We then plug in the equilibrium value for n when the species is present (=K):

d(- n ln(n/K))/dn |_n=K = - ln(K/K) - = - , using the fact that ln(1)=0.

Since this is a model in continuous time, stability of the equilibrium is guaranteed if this derivative is negative (ie when is positive). In this case, a perturbation away from the equilibrium decreases in size over time.

Conversely, the equilibrium will be unstable if the derivative is positive (ie when is negative). In this case, a perturbation away from the equilibrium increases in size over time.

To find the global solution, we perform a change of variables from n to y=ln(n/K) in the Gompertz equation. That is, we set n=K e^y in the equation to get:

d(K e^y)/dt = - K e^y ln(K e^y/K) = - K e^y y

But d(K e^y)/dt = K e^y dy/dt so

K e^y dy/dt = - K e^y y

Dividing both sides by K e^y, leads to:

dy/dt = - y

This is the same equation as in the exponential growth model. It can be solved in the exact same manner, by separation of variables. Moving dt to the left hand side and y to the right hand side, we get:

dy/y = - dt

Integrating both sides:

ln(y) = - t + c

where c is some constant of integration. Therefore,

y = e ^{- t +c} = c e ^{- t}

(where c is now some other constant).

This gives the general solution in terms of y, in terms of n, we have:

ln(n/K) = c e^{- t}

At t=0, we get ln(n₀/K) = c, which gives us a solution for c:

ln(n/K) = ln(n₀/K) e^{- t}

Solving this equation for n gives:

n/K = Exp[ln(n₀/K) e^{- t}] = Exp[ln(n₀/K)]^x

where x = e^{- t}. Therefore:

n = K (n₀/K)^x.

x[t+1] = (1-) x[t]

y[t+1] = x[t] + y[t].

These are linear equations that can be described by a transision matrix: {{(1-), 0},{,1}}.

The eigenvalues of this matrix are (1-) and 1 and their associated eigenvectors are {1,-1} and {0,1}.

We can perform the matrix operation: AD^tA.{x[0],y[0]} to find the values of x[t] and y[t]:

x[t] = x[0] (1- )^t

y[t] = x[0] (1-(1- )^t)+y[0]

Since x[0]=1 and y[0]=0, these equal

x[t] = (1- )^t

y[t] = (1-(1- )^t)

NOTE: You could also figure this out on the basis of probability reasoning. For a cell to be non-mutant at cell generation t, it had to not undergo any mutations in any of the t cell divisions, which will happen with probability (1- )^t. 1 minus this quantity is therefore the probability that the cell will be mutant.

When = 10^-7, y[100] is very nearly 10^-5, i.e. there will be very few mosaic cells at a particular gene.

Across all of the genes in the genome with = 10^-2 mutations per cell division, y[100] is about 0.63, i.e. there will be very many mosaic cells that contain changes at some gene in the genome.

First, we will solve this problem in the presence of red squirrels.

We have to figure out m₀, the number of offspring born in the next year to individuals that were just born. This will equal the probability of surviving until the next year (0.25*0.5) times the expected number of offspring (4), so m₀=0.5 in the absence of red squirrels.

m₁, the number of offspring born in the next year to individuals that are currently one-year olds, is equal to the probability of surviving until the next year (0.5) times the expected number of offspring (8), so m₁=4.

Finally, the probability of surviving from age class 0 to age class 1 is 0.25*0.5 = 0.125, in the absence of red squirrels.

The Leslie matrix in this case is: {{0.5, 4},{0.125,0}}.

The eigenvalues of this matrix are 1 and -0.5. The largest eigenvalue is 1 and therefore the population will remain roughly constant in size over time. The eigenvector associated with this eigenvalue is {0.89, 0.11} (normalized to sum to one). You conclude that 89% of the individuals in the summer census should be newborn.

Now, you analyse the case with red squirrels absent. The parameters of the Leslie matrix become:

m₀ = 4*0.75*0.5 = 1.5

m₁ = 8*0.5 = 4

p₀ = 0.75*0.5 = 0.375

The Leslie matrix in this case is: {{1.5, 4},{0.375,0}}.

The leading eigenvalue is now 2.19 and its eigenvector would be {0.85,0.15}. This suggests that the population would increase dramatically (doubling in size every year) if the red squirrels were removed and that a higher proportion of yearlings would be seen in the population.

The point is stable since as time passes the population approaches the equilibrium. It is actually globally stable since the point is approached over time regardless of the starting conditions.

(NB - The terminology is tricky here since the total number of individuals in the system may depend on the exact starting conditions, but the ratios among all the variables reach a fixed quantity.)

There is no need to do a local stability analysis, since for linear models the local stability matrix is the same as the transition matrix (try it!). Studying the transition matrix already tells you everything you need to know about how the population will change near the equilibrium.

For the linear sets of equations, you would first write {n₁[t+1], n₂[t+1]} as the matrix product of a matrix, M, and the vector {n₁[t], n₂[t]}. You then want to find M^t, which is easiest to find by determining the eigenvalues (placing these along the diagonal of a matrix D) and eigenvectors (placing these in the columns of a matrix A), and then determining the matrix product: AD^tA^-1. This product equals M^t and, when multiplied by {n₁[0], n₂[0]}, describes the position of the population at time t, {n₁[t], n₂[t]}. By analysing what happens over time, you can get a sense of the dynamics of the system and can determine the equilibria.

For non-linear sets of equations, there is no general transition matrix that does not contain n₁[t] and/or n₂[t]. However, if you find the equilibria of the system, you can approximate the dynamical equations near the equilibria by finding the local stability matrix (the matrix of partial derivatives evaluated at the equilibrium). If this local stability matrix has any eigenvalue greater than one in magnitude, the equilibrium is unstable. If all eigenvalues are less than one, the equilibrium is stable. If the leading eigenvalues are complex, then you would observe cycling around the equilibrium (these cycles may spiral in or out from the equilibrium depending on the eigenvalues). Although this analysis identifies the equilibria and their stability, it does not tell you what happens when the system starts very far from the equilibrium. It is generally good to simulate the dynamics away from equilibrium to infer the global behavior of the system.

Near this equilibrium, we can approximately describe the dynamics using a linear stability matrix (the matrix of partial derivatives evaluated at the equilibrium).

In this case, the local stability matrix is:

Another occurs when n₁ = 0 and n₂ = (a₂-1)/b₂.

Another occurs when n₁ = (a₁-1)/b₁ and n₂ = 0.

Finally, the only equilibrium with both species present occurs when n₂ = (b₂a₁ - c₁a₂ + c₁ - b₂)/( b₁b₂ - c₁c₂) and n₂ = (b₁a₂ - c₂a₁ + c₂ - b₁)/( b₁b₂ - c₁c₂).

(b) The local stability matrices must be determined by finding the partial derivatives and plugging in the equilibria found in the previous equation.

For n₁ = 0 and n₂ = 0, this gives:

For n₁ = 0 and n₂ = (a₂-1)/b₂, the local stability matrix is:

For n₁ = (a₁-1)/b₁ and n₂ = 0, the local stability matrix is:

(c) Since a₁ and a₂ are both greater than one, the equilibrium with n₁ = 0 and n₂ = 0 is unstable. The eigenvalues for the case with n₁ = 0 and n₂ = (a₂-1)/b₂ are 0.94 and 0.926 so this equilibrium is stable. The eigenvalues for the case with n₁ = (a₁-1)/b₁ and n₂ = 0 are 1.00099 and 0.8039 so this equilibrium is stable.

Species 1 (S. cerevisiae) is unable to invade the equilibrium with n₁ = 0 and n₂ = (a₂-1)/b₂ primarily because the value of c₁ is so high. This means that there is strong interspecific competition with S. pombe. S. pombe strongly suppresses the growth of S. cerevisiae.

Interestingly, the growth rate of S. cerevisiae is higher and so in Gause's experiments he observed a much more rapid increase in S. cerevisiae. The theory predicts, however, that had these experiments been run for longer periods of time, S. pombe would have displaced S. cerevisiae once it became established.

(b) If we encounter 1 rabbit every 1.5 hours, then that means we'll encounter 0.67 rabbits every hour (pretty gory). We need to integrat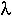e e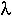^{- x} = 0.67 e^{-0.67 x} between hours 7 and 8. This gives 0.0045 (unlikely, since we'll probably encounter the first one much earlier in the day). The exponential distribution applies to this problem, since we are waiting for the first event to occur when events happen randomly and continuously over time.

(c) P = 0.999⁵⁰⁰ = 0.606 for zero errors. P = 500*0.999⁴⁹⁹*0.001 = 0.303 for one error. P = 1-0.606-0.303 = 0.091 for more than one error. This problem describes a binomial distribution. Alternatively, since the probability of an error is small, you could use a Poisson distribution to answer this problem.

(d) E[X] = 10/0.1 = 100 minutes since 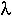= 0.1 fish per minute. Var(X) = r/ 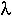² = 10/0.01 = 1000 so the standard deviation is 31.6 minutes. From the normal approximation, the 95% confidence limits around the mean of 100 minutes is 100-2*31.6 to 100+2*31.6, or roughly 40 to 160 minutes until you go home.

(a) Binomial distribution: All integers from 0 to n.

(b) Exponential distribution: All real numbers from 0 to infinity.

(c) Negative Binomial distribution: All integers from r to infinity (note that you must wait at least r trials before observing the r^th positive outcome).

(d) Normal distribution: All real numbers from negative to positive infinity.

(e) Geometric distribution: All integers from 1 to infinity (note that you must wait at least one trial before observing the first positive outcome).

(f) Gamma distribution: All real numbers from 0 to infinity (note that all r positive outcomes could, at least in theory, occur very near the beginning of the observation period).

Mean of exponential = 1/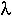

Variance of geometric = (1-p)/p²

Variance of exponential = 1/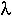²

Therefore, if 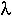(the instantaneous rate of events per time unit) is equal to p (the probability of an event in a given time unit) and if p is small, then the geometric and exponential distributions converge.

This makes sense, since if p is small, then there should be little difference between observing events over specific time periods (eg every day) or continuously over time. When the event will first be seen is roughly the same in either case.

In contrast, if 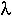is very large, you could see an event instantaneously in the continuous case, but you would have to wait for one time unit to pass in the discrete case.

[Notice that as 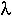goes to infinity, E[X] for the exponential distribution goes to zero. But as p goes to one (its maximum) E[X] for the geometric goes to one.]

Notice that the integral goes from 0 to infinity. Since the exponential distribution measures the time until first occurrence of an event, it cannot be negative.

To solve we must integrate by parts. Let u=x and dv equal the rest of the integral. Then, we get:

The tricky part here is to recognize that e^-x goes to zero rapidly as x goes to infinity. Exponential decay is so rapid that even x e^-x goes to zero as x goes to infinity (despite the fact that x in this equation is going to infinity).