
Logistic Growth in Discrete Time



This suggests that we must change the assumption that each individual will have the same number of offspring on average (R), regardless of the population size.
The expected number of offspring may depend on the population size in any number of ways.
The logistic equation assumes that the expected number of offspring decreases linearly with the population size:
 A parent has one offspring on average if r=0 or if (1 - n[t]/K)=0,
which will be true if n[t]=K.
A parent has one offspring on average if r=0 or if (1 - n[t]/K)=0,
which will be true if n[t]=K.
r is known as the intrinsic rate of growth since it measures whether the population tends to grow (r>0) or shrink (r<0).
K is known as the carrying capacity since it measures the population size at which the population produces exactly enough offspring to just replace itself.


This is the recursion equation describing the change in population size from generation to generation under the logistic model.
This recursion is
[Non-linear means that there is a term in the equation where the variable is taken to some power other than 1].
The change in population size from one generation to the next is:
 n = n[t+1] - n[t] = r (1 - n[t]/K) n[t]
n = n[t+1] - n[t] = r (1 - n[t]/K) n[t]When will the population grow in size?


If there are n[t] individuals in the population at time t, then the rate of change of the whole population size will be:
This is the differential equation describing the rate of change in population size in the logistic model.
If K were infinity, n[t]/K would be zero and the population growth would follow the equation for exponential growth.
If the population size, n[t], were much smaller than the carrying capacity, K, then n[t]/K would be small. In this case, the population would grow nearly exponentially (until the population size were no longer much smaller than K).


Mathematical Aside: Definition of the derivative
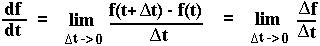
According to the discrete time model, as long as r is small, the population will change (approximately) by:
 n = r (1 - n[t]/K) n[t]
n = r (1 - n[t]/K) n[t]
 t
t
over the time interval  t near generation t as long as
t near generation t as long as  t is not too long.
t is not too long.
Using the definition of the derivative, we can use this equation to define the derivative of the population size with respect to time in the discrete model:
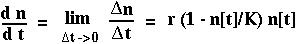
If r is large, however, then the population can change in size rapidly over short periods of time and the discrete and continuous time models give VERY DIFFERENT answers.


She observed the following growth curves for the two types of cells:
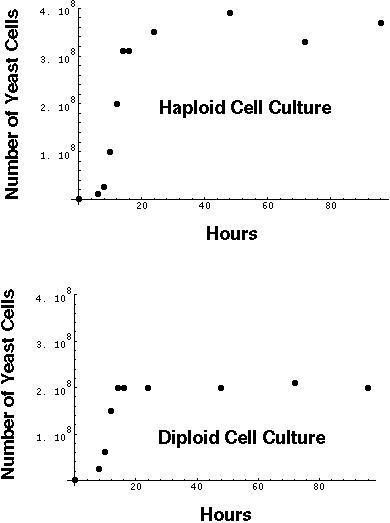
Although the population grows nearly exponentially at first, growth decreases as the population size increases (density dependent growth is observed).
The equilibrium population size (K) is larger for the haploid cells, but do haploid and diploid cells have different intrinsic rates of increase (r)?
By fitting the logistic equation to the data:
r(haploid) = 0.62
K(diploid) = 2.0 108
r(diploid) = 0.57
Using these parameter estimates with the logistic model does provide an excellent fit to the data:
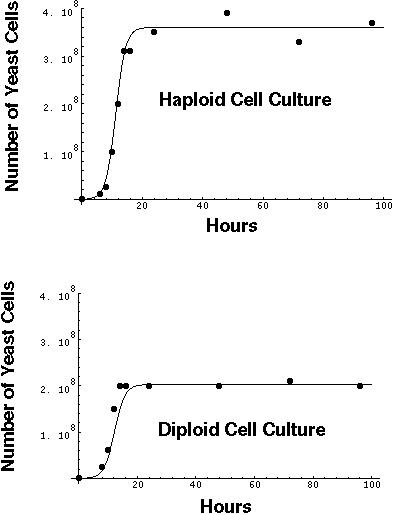
[Note: This fit may be a bit misleading, though, since such excellent fits are not generally observed outside of the laboratory with organisms other than microorganisms.]