Non-Linear Equations
We now turn our attention to models that describe the dynamics of a system in terms of NON-LINEAR equations in more than one variable.
With occasional exceptions, non-linear systems of equations do not yield general solutions (i.e. they are often intractable).
Other methods of analysing equations therefore become especially important, including
N1[t+1] = N1[t] - r1 N1[t] + ρ1 N1[t] N2[t]
N2[t+1] = N2[t] - r2 N2[t] + ρ2 N1[t] N2[t]
where the r's are the exponential decline rates for each species when the other species is absent (assumed positive) and the ρs are the benefits of cooperation (also assumed to be positive).
This model cannot be solved generally, so to determine what will happen over time we will conduct the same combination of techniques applied to one-locus models: use graphs, calculate equilibria, and determine stability to paint a picture of how the system behaves.
Preliminary Graphical Analysis
The first step of an analysis might be to graph examples to see what happens to each of the species under different parameter conditions:
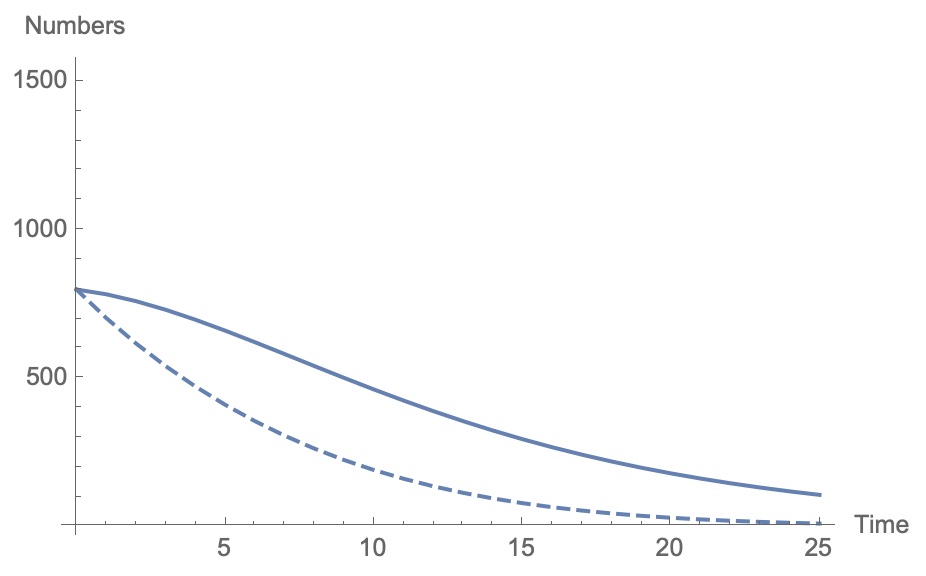
Here, the number of species 1 is solid and the number of species 2 is dashed. In this example, r1 = 0.1, r2 = 0.2, ρ1 = 0.0001, ρ2 = 0.0001 and the populations both decline.
Such a graphical method is only useful for specific examples, however, and doesn't give us a general picture of what will happen and when.
Identification of Equilibria
As before, we determine equilibria by finding out when the variables will stay constant over time.
Unlike the case of a single variable and a single function, however, we must find an equilibrium solution where ALL of the variables remain constant over time.
For a continuous model, this requires that dN1/dt = 0 AND that dN2/dt = 0.
For a discrete model, this requires that N1[t+1] = N1[t] AND that N2[t+1] = N2[t].
To get both species to persist at equilibrium requires that both N1[t+1] = N1[t] and N2[t+1] = N2[t].
To solve both equations simultaneously, we thus must find solutions to:
= - r1 + ρ1 
= - r2 + ρ2
The first equation can be satisfied if either = 0 or if = r1/ρ1. But this isn't an equilibrium! It is only two ways of making sure that N1[t+1] = N1[t].
To ensure that we also don't see changes in the number of species 2, we also need N2[t+1] = N2[t]. This requirement can be satisfied if either = 0 or if = r2/ρ2.
An equilibrium is a point (, ) at which neither variable changes.
In this case, there are two combinations that work and that are equilibria:
= 0 and = 0
= r2/ρ2 and = r1/ρ1
Only at these points will BOTH species be present in constant numbers over time.
The next step is to determine when the different equilibria are STABLE and when they are UNSTABLE (at least locally).
We have already learned how to perform a local stability analysis for a single non-linear equation in one variable. Let's review.
DISCRETE MODEL
Say that the population is currently a small distance (
) away from the equilibrium. We use the Taylor Series to determine whether this perturbation will grow or shrink.
Let f(p[t]) be the recursion equation giving p[t+1] as a function of p[t]. Then:
)| > 1
)| < 1
) > 0
) < 0
)| < 1 in a discrete model, since a perturbation from the equilibrium shrinks over time.
We also learned how to do a local stability analysis for a one-variable model in continuous time. In that case, we found that a perturbation would
) > 0
) < 0
) < 0 in a continuous model.
How do we generalize this to a system of equations in more than one variable???
In the following, we will focus on a system of equations in discrete time. To learn how to analyse the stability of an equilibrium for a system of equations in continuous time, read Roughgarden pp. 572-577.
First of all, we have to learn how to do the Taylor Series when we have more than one variable.
Mathematical Aside: Taylor Series in Multiple Variables
Let x1[t+1] be written as some function (f1) of all the variables in the previous generation: f1(x1[t],x2[t],...xn[t]). The Taylor Series of this equation is:
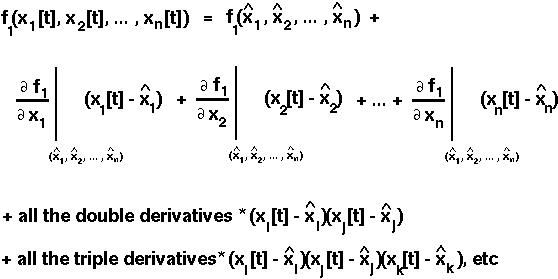
Notice that if we only had one variable (x1[t]), then the Taylor Series would be the same as before.
To make the Taylor Series more useful for our purposes, let's assume that the population is near an equilibrium point. This will allow us to ignore the double derivatives and higher derivatives, since these are multiplied by very very small terms (squares and higher of terms).
Then:
PHEW!
This last equation gives us the perturbation of the first variable from its equilibrium value in the next generation as a function of the partial derivatives of f1 and the perturbations of all the variables in the previous generation.
The perturbation of the second variable will be described by a similar equation, except that f1 would be replaced by f2, etc.
NOTICE: What we have done is taken the NON-LINEAR equations (f1, f2, ... , fn) and turned them into LINEAR APPROXIMATIONS near the equilibrium we are interested in.
In the model of cooperative brooding with two species, we have two recursion equations which are:
N1[t+1] = N1[t] - r1 N1[t] + ρ1 N1[t] N2[t]
N2[t+1] = N2[t] - r2 N2[t] + ρ2 N1[t] N2[t]
The Taylor Series of the first one gives:
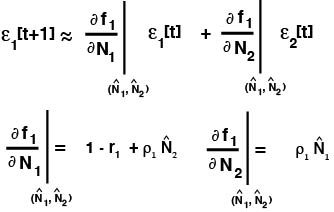
and the Taylor Series of the second one gives:
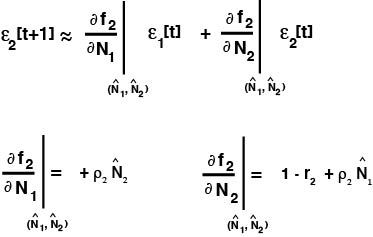
Now we're ready for business.
There are two possible equilibria whose stability we want to determine. First, let's work on the simplest one with both N1 and N2 equal to zero (both populations are extinct).
Both species extinct at equilibrium
The dynamics near this equilibrium can be written in MATRIX form:
| 1-r1 | 0 |
| 0 | 1-r2 |
Because this is a diagonal matrix, the eigenvalues are the diagonal elements: 1-r1 and 1-r2. [This rule is true too for triangular matrices with all zeroes below the diagonal or all zeroes above the diagonal and is a handy rule!]
From what we know about matrices, when will this perturbation vector grow over time?
If the leading eigenvalue is greater than one!
But the eigenvalues in this case are (1-r1) and (1-r2). Because the growth rates were assumed to be positive the leading eigenvalue will never be greater than one. Furthermore, both (1-r1) and (1-r2) must be positive for the number of each species to be positive in the next generation when the other species is absent (reasonable), so we don't expect oscillations. This equilibrium should be stable.
Both species present at equilibrium
Second, let's consider the other equilibrium where both species are present, with = r2/ρ2 and = r1/ρ1.
The dynamics near this equilibrium can be written in MATRIX form:
| 1-r1+ρ1 |
ρ1 |
| ρ2 |
1-r2+ρ2 |
Plugging in the equilibria, this simplifies down to:
| 1 | ρ1 r2/ρ2 |
| ρ2 r1/ρ1 | 1 |
Calculating the eigenvalues of this matrix, Det(M - λI), and using the quadratic formula to calculate these eigenvalues, we find that λ = 1 +/- √(r1 r2). Because the r's are positive, the largest of these eigenvalues, 1 + √(r1 r2), must be larger than one. Hence, this matrix stretches the perturbation over time, so that the system moves away from the equilibrium, which is unstable.
Overall, the only stable equilibrium is when both species are extinct. Let's explore graphs (in class) to see what is going on!
[In short: if there are too few individuals of each species to find each other and cooperate much, the pair of species goes extinct; if there are enough individuals to help that the species are able to grow, then they continue to grow to infinity...or at least until resources run out, which is a limitation not built into the model.]
Back to biology 301 home page.