Ornstein-Uhlenbeck calculations differ between geiger and diversitree for non-ultrametric trees, when calculations in diversitree are carried out with the "pruning" method. This shows what is going on.

This was brought to my attention by Dave Bapst

First, load the packages.

library(diversitree)

## Loading required package: deSolve

## Loading required package: ape

## Loading required package: subplex

library(geiger)

## Loading required package: MASS

## Loading required package: mvtnorm

## Loading required package: msm

## Loading required package: ouch

## Loading required package: methods

Here is a simple non-ultrametric tree.

set.seed(2)
tree <- rtree(100)

plot(tree, no.margin=TRUE)

Simulated non-ultrametric tree

And here is a random trait (evolved under Brownian motion with a rate of .1)

x <- rTraitCont(tree)

cols <- colorRamp(c("lightgrey", "darkblue"))((x - min(x))/diff(range(x)))
cols <- rgb(cols[,1], cols[,2], cols[,3], maxColorValue=255)
plot(tree, no.margin=TRUE, label.offset=.2)
tiplabels(pch=19, col=cols)

Simulated non-ultrametric tree

Brownian motion (to check)

This makes a likelihood function using the same algorithm as geiger:

lik.bm.v <- make.bm(tree, x, control=list(method="vcv"))

While this uses the pruning algorithm

lik.bm.p <- make.bm(tree, x, control=list(method="pruning"))

Maximise the likelihoods:

fit.bm.v <- find.mle(lik.bm.v, .1)
fit.bm.p <- find.mle(lik.bm.p, .1)

And fit the same model with geiger

fit.bm.g <- fitContinuous(tree, x)

## Fitting  BM model:

The diversitree methods give the same answer (even taking the same number of steps -- the likelihood calculations should agree exactly).

all.equal(fit.bm.v, fit.bm.p)

## [1] TRUE

We seem to have found the same peak as fitContinuous (to the sort of tolerances expected)

all.equal(fit.bm.g$Trait1$lnl,  fit.bm.v$lnLik)

## [1] "Mean relative difference: 3.846e-06"

The estimated parameters differ a little...

all.equal(fit.bm.g$Trait1$beta, fit.bm.v$par, check.attributes=FALSE)

## [1] "Mean relative difference: 0.003727"

fit.bm.g$Trait1$beta - fit.bm.v$par

##        s2 
## 3.398e-05 

...but when evaluated in the same place, the answers are essentially identical (therefore, any difference is due to the optimisation, not the likelihood evaluation).

p.g <- fit.bm.g$Trait1$beta
lik.bm.v(p.g) - fit.bm.g$Trait$lnl

## [1] -5.684e-14

lik.bm.p(p.g) - fit.bm.g$Trait$lnl

## [1] -2.842e-14

lik.bm.v(p.g) - lik.bm.p(p.g)

## [1] -2.842e-14

Ornstein-Uhlenbeck on non-ultrametric trees.

The vcv method here is almost directly taken from geiger. The main difference is that it is easy to evaluate the likelihood function at any parameter vector.

lik.ou.v <- make.ou(tree, x, control=list(method="vcv"))

Here is the pruning algorithm. I'm using the "C" backend, as it is quite a bit faster than the pure-R version (though less well tested, beware -- in particular, in diversitree 0.9-3 this gives incorrect answers on non-ultrametric trees, though backend="R" works fine).

lik.ou.p  <- make.ou(tree, x,
                     control=list(method="pruning", backend="C"))

These functions both take three arguments; diffusion, restoring force and optimum.

argnames(lik.ou.p)

## [1] "s2"    "alpha" "theta"

Before going anywhere, show that these give the BM fit when "alpha" is zero (or "very small" in the VCV-based calculation).

fit.bm.v$lnLik

## [1] 90.49

lik.ou.v(c(coef(fit.bm.v), 1e-8, 0))

## [1] 90.49

lik.ou.p(c(coef(fit.bm.v), 0, 0))

## [1] 90.49

(Note that we have to provide a nonzero alpha parameter to fit.bm.v or calculations will fail:

lik.ou.v(c(coef(fit.bm.v), 0, 0))

## Error: system is computationally singular: reciprocal condition number = 0

We also have to provide a theta value, though with alpha of 0, this is ignored.

Then maximise the likelihood. This takes quite a bit of time (and 5,000 function evaluations) as the parameters are horrendously correlated here

fit.ou.v <- find.mle(lik.ou.v, c(.1, .1, .1))
fit.ou.p <- find.mle(lik.ou.p, c(.1, .1, .1))

Again, fit the model under geiger, too.

fit.ou.g <- fitContinuous(tree, x, model="OU")

## Fitting  OU model:

First, the VCV-based calculation and geiger agree, which is good, as they're basically the same set of code:

all.equal(fit.ou.g$Trait1$lnl, fit.ou.v$lnLik)

## [1] TRUE

But the pruning calculation differs:

fit.ou.g$Trait1$lnl

## [1] 90.73

fit.ou.v$lnLik

## [1] 90.73

fit.ou.p$lnLik

## [1] 92.8

(note that these are log likelihoods, not negative log likelihoods, so the higher value of 92.8 is better than the lower value of 90.7).

Extract the parameters from the geiger fit

p.g <- with(fit.ou.g$Trait1, c(beta, alpha))

To tolerable accuracy, the VCV based approach has found the same pair of parameters as geiger:

all.equal(fit.ou.v$par[1:2], p.g, check.attributes=FALSE)

## [1] "Mean relative difference: 2.239e-05"

(the theta value is currently ignored in the VCV fit, so I'm just comparing the first two values)

Again, at the same point these agree very well.

lik.ou.v(c(p.g, 0)) - fit.ou.g$Trait1$lnl

## [1] 5.684e-14

Vary the theta parameter and see how this affects the likelihood. xx is a range of possible optima that span the observed range of values.

xx <- seq(min(x), max(x), length=201)

This makes a function with only parameter "3" free, and the others set to p.g (geiger's optimum)

f <- constrain.i(lik.ou.p, c(p.g, 0), 3)

Evaluating at each of the thetas:

yy <- sapply(xx, f)

plot(yy ~ xx, type="l", xlab="theta", ylab="Log-likelihood", las=1)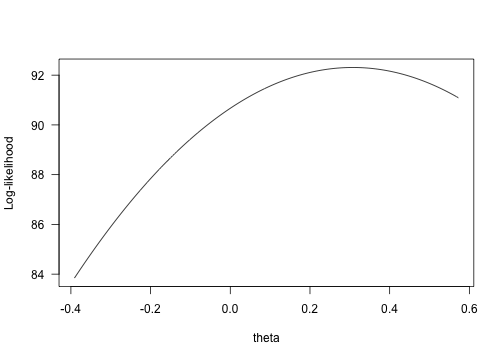

log-likelihood vs. theta

Intersects at about 0.0057:

g <- approxfun(xx, yy - fit.ou.v$lnLik)
xg <- uniroot(g, range(xx))$root
xg

## [1] 0.005665

Wheras we find a ML theta at 0.31

xd <- optimise(g, range(xx), maximum=TRUE)$max
xd

## [1] 0.3075

plot(yy ~ xx, type="l", xlab="theta", ylab="Log-likelihood", las=1)
abline(h=fit.ou.v$lnLik, v=xg, col="red")
abline(h=f(xd), v=xd, col="blue")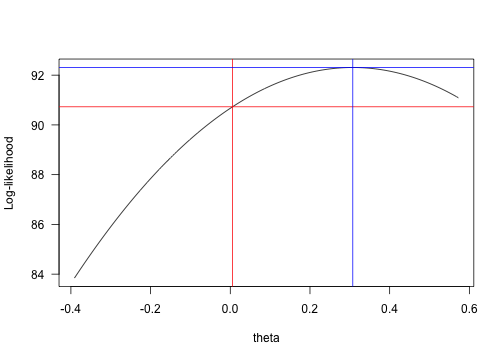

log-likelihood vs. theta

So, the difference probably lies in the treatment of the root state and/or the optimum. Let's see what geiger is doing. We need two functions though:

phylogMean <- geiger:::phylogMean
ouMatrix   <- geiger:::ouMatrix

Then, compute the mean like so (in geiger's OU, I believe that this is both the optimum and the root state):

mu <- c(phylogMean(p.g[1] * ouMatrix(vcv.phylo(tree), p.g[2]), x))

mu is about 0.01, which is similar to the blue vertical line.

mu

## [1] 0.01852

If we plug in mu as both the optimum parameter and the root state, we get geiger's likelihood:

lik.ou.p(c(p.g, mu), root=ROOT.GIVEN, root.x=mu)

## [1] 90.73

lik.ou.v(c(p.g, NA))

## [1] 90.73

Now, is that the best likelihood subject to that constraint? To find this out, we have to make a new likelihood function that automatically sets the root state to the optimum, given the current parameters. This function does this:

lik.ou.c <- function(x)
  lik.ou.p(x, root=ROOT.GIVEN, root.x=x[3])

Run an ML search from the geiger ML point and the mu value found above:

p.c <- c(p.g, mu)
names(p.c) <- argnames(lik.ou.p)
fit.ou.c <- find.mle(lik.ou.c, p.c, method="subplex")

Yes! It is the same.

fit.ou.c$lnLik

## [1] 90.73

all.equal(fit.ou.c$lnLik, fit.ou.v$lnLik)

## [1] TRUE

In the Hansen paper, there is a bit about how the statistic that they present is a "restricted ML estimator". It's possible that the above transformation is what makes it one.

Document details

Document compiled on 2012-05-10 21:40:50 PDT With R version and diversitree version 0.9.4. Original source: ou-nonultrametric.R

examples, diversitree home