


For, unless advantageous mutations occur so seldom that each has had time to become predominant before the next appears, they can only come to be simultaneously in the same gamete by means of recombination.
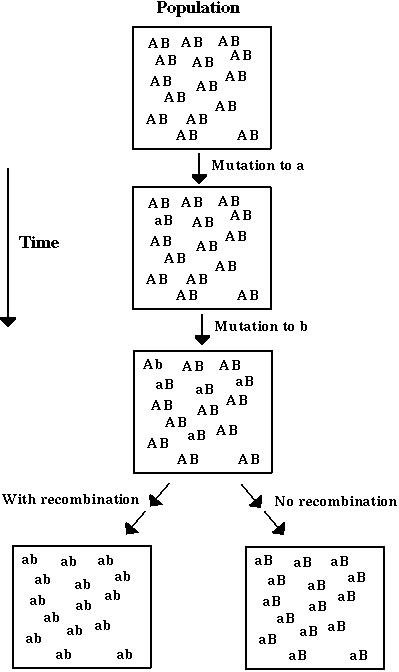


This is generally thought to be a group selection argument.
We have examined the evolution of a population with genetic variation for recombination to determine whether increased recombination can be favored within a population by individual-level selection.
Fisher-Muller hypothesis (Take 2): New beneficial mutations will have a higher probability of fixation, P, if there is recombination than if there isn't.
Modifier alleles that increase recombination will therefore tend to be associated with beneficial alleles that have a higher chance of fixation.
As the successful beneficial alleles spread, the modifier alleles that increase recombination are dragged along by hitchhiking.


Selection: Assumed to depend multiplicatively on genotype at two genes (A and B).
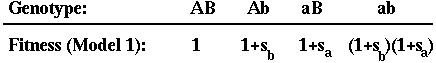
Recombination: Occurs between the two genes (A and B) at a rate that depends on the alleles carried a third modifier gene (M):

The modifier gene recombines with the nearest selected gene (A) at a rate R.


Calculating the Probability of Fixation: We assume that an individual carrying a new beneficial mutation has a mean number of offspring (1+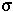 ) that is greater than the replacement rate (1) and that the offspring distribution is Poisson.
) that is greater than the replacement rate (1) and that the offspring distribution is Poisson.
The fixation probability of a beneficial allele that arises at time t is:
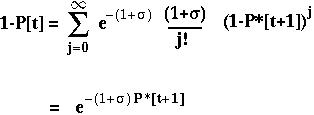
P*[t+1] is the expected fixation probability of a single copy of the allele in an offspring.
With only one gene, P*[t+1] equals P[t] and
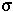 equals s:
equals s:
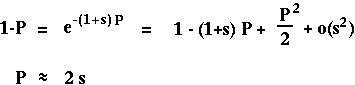
(Classical result from Haldane 1927.)


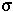 , depends on which allele it appears with at gene B.
, depends on which allele it appears with at gene B.
Furthermore, the fixation probability of an offspring copy, P*[t+1], is no longer equal to the fixation probability of the parental copy, since recombination may place the mutant allele onto a different genetic background.
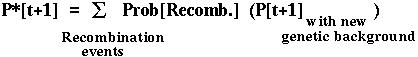
Since there are four genetic backgrounds (MB,Mb,mB,mb), this approach leads to four equations describing how the probability of fixation of an allele changes over time.
These equations can be solved numerically and can be approximated analytically (by assuming that selection is weak and replacing the difference equations with differential equations).


 Barton (1995) showed that recombination always increases the fixation probability of a beneficial mutant in this model.
Barton (1995) showed that recombination always increases the fixation probability of a beneficial mutant in this model.
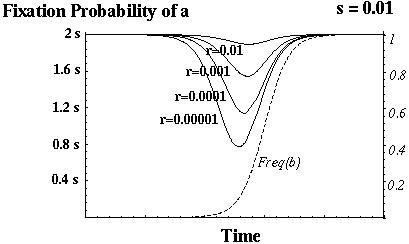
 Otto & Barton (1996) showed that modifier alleles that increase recombination always increase in frequency.
Otto & Barton (1996) showed that modifier alleles that increase recombination always increase in frequency.
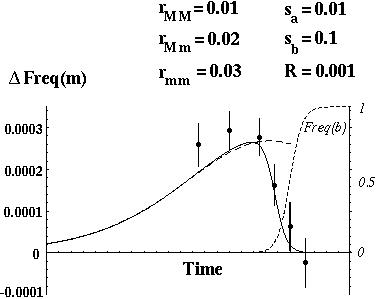
 The selection for increased recombination is only strong, however, if the genes are tightly linked or if there are beneficial alleles segregating at many different genes.
The selection for increased recombination is only strong, however, if the genes are tightly linked or if there are beneficial alleles segregating at many different genes.