Allais paradox
Instructions
Please choose between:
A: A chance of winning
4000 Euro with probability 0.2 (expected value 800 Euro)
B: A chance of winning
3000 Euro with probability 0.25 (expected value 750 Euro)
Please choose between:
C: A chance of winning
4000 Euro with probability 0.8 (expected value 3200 Euro)
D: A chance of winning
3000 Euro with certainty.
Evaluations
Number of players: 25
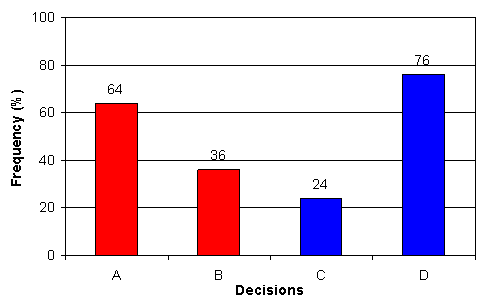
Frequency of different decisions:
Comments
In large scale experiments,
most players (about 70%) choose 4000 Euro with probability 0.2 (A) rather
than 3000 Euro with probability 0.25 (B). And indeed, the expected value
4000 Euro with probability 0.2 (800 Euro) is larger than of 3000 Euro with
probability 0.25 (750 Euro). In the second decision, most choose 3000 Euro
with certainty (D). This is paradox. First of all, the expected value of
C, 4000 Euro with probability 0.8 (3200 Euro), is larger than that of D,
3000 Euro with certainty (3000 Euro). More puzzling still, the values in
the first decision are obtained from those in the second decision simply
by reducing the odds by the factor 4. It is as if we first tossed two coins
and do the second decision only if both show heads.
Addendum (November 10, 2003)
The irrational switching behavior of the majority of participants
can be illustrated in an even more striking way by showing the percentage of participants
that chose A in the first round and C in the second, those that chose first A
then D, B then C and finally B followed by D. Evaluations
Number of players: 25
Frequency of different pairs of decisions: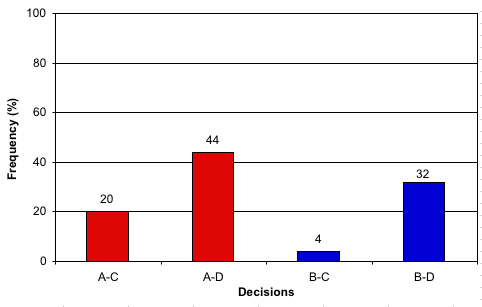 
Comments
As expected, the majority of people (44%) choose first A and then D. 20%
make the rational choice of A followed by C. Somewhat surprising is the considerable
percentage that is extremely risk averse and chooses B and then D. Only a single
individual chose first B and the C - might be simply a miscalculation.
Written by Christoph Hauert