Assume that there are N diploid individuals in a population (constant over time!). Each individual carries two alleles, so there are 2N alleles within a population.

(NOTE: We're keeping track of the separate DNA molecules and not whether they're the same sequence of basepairs or not.)

2N offspring alleles are chosen from the 2N parent alleles randomly with replacement.

The probability that two individuals will have the same parent is 1/(2N). This is called a "coalescent event": two alleles in the current generation trace back to a single DNA molecule in the previous generation.

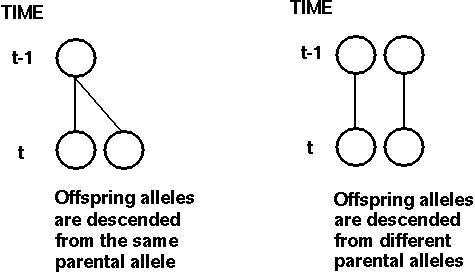
Because this probability does not change over time if the population is constant and if the alleles have not coalesced, the time until two alleles coalesce will be given by a geometric distribution, with a mean of 2N generations.

For n alleles to each have different parent alleles in the previous generation, the second allele has to have a different parent allele (Prob=1-1/2N), the third allele has to have a different parent allele than either the first or the second (Prob=1-2/2N), etc:

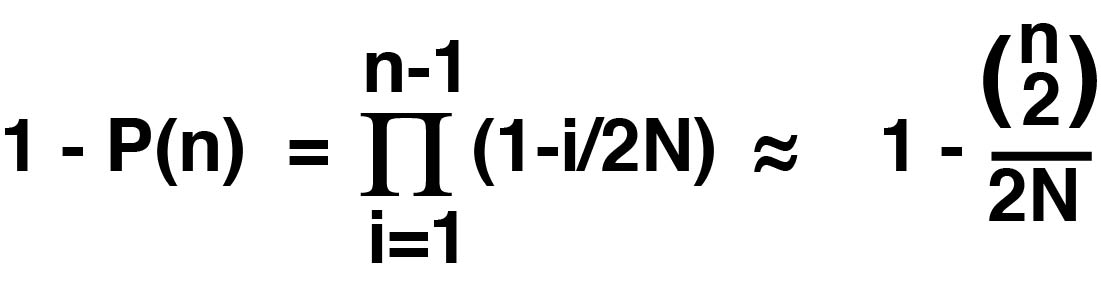
1-P(n) is the probability that there will not be a coalescent event in the previous generation in a sample of n alleles, and P(n) is the probability of a coalescent event (the chance that more than one coalescent happens in a generation can be ignored if n<<2N).

If in each generation, the probability that there is a coalescent event is P(n), then the expected time until the first "success" (ie first coalescent) follows a geometric distribution:

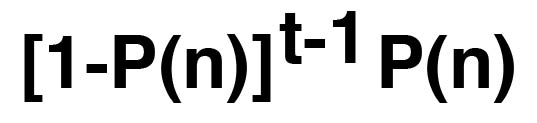
That is, the expected time until the first coalescent event is simply .

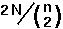This is extremely useful. For instance, we can use it to find the expected time until all of the alleles have coalesced from the sum:

.

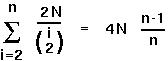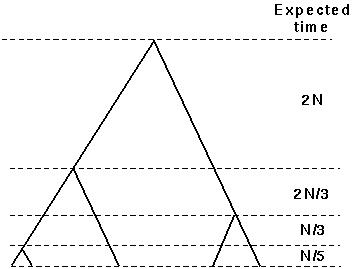
The time it takes for a sample of 2 alleles to coalesce is about 2N generations. And for many alleles in the sample it takes about 4N generations.

.

This illustrates cool facts about the coalescent process:

• Coelescent events happen rapidly when there are many lineages
• Coelescent events happen much more slowly when there are few lineages

Key assumptions: The population remains constant, with the number of offspring per parent following a Poisson distribution.