Solving Linear Equations
Aim: To use matrix notation to determine how the number of methylated sites changes over time.
We will track the number of methylated CpG sites (x[t]) and unmethylated sites (y[t]) at time t.
Recall that
equals the proportion of methylated sites that remain methylated per cell division (maintenance methylation)
equals the proportion of unmethylated sites that become methylated per cell division (de novo methylation)
Under these definitions, the number of methylated and unmethylated sites in the next cell generation equal:
x[t] + y[t]) x[t] + (1-) y[t]Step 1: These equations are linear functions of the variables and so can be written in matrix form:
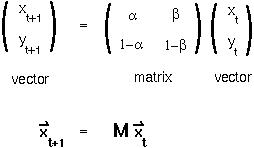
To avoid having to take the matrix M to the t power (!!), we will find the coordinate system in which which the transition matrix is a diagonal matrix.
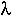=1 and
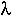=-Step 3: A diagonal matrix D which is similar to M is:
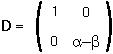
Step 4: Find the two eigenvectors of the matrix M:
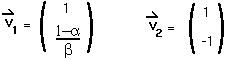
Step 5: Therefore the transformation matrix, A, is :
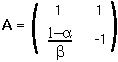
Matrix A changes the coordinate system to one in which the transition matrix is diagonal.
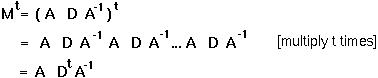
and we can write the general solution as:
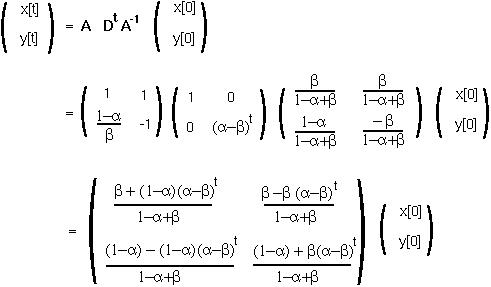
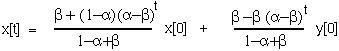
Since (-) is between -1 and 1, as t goes to infinity, x[t] will go towards the equilibrium value of:
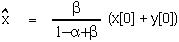
At this point, we can use the equilibrium value to write the equation in a much simpler form:
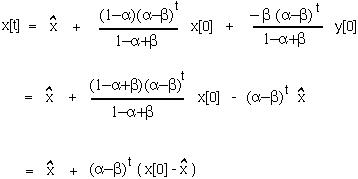
This is exactly the same solution that we obtained by analysing the problem using a one variable model.
Notice that we never did use the fact that x and y measure the numbers of methylated and unmethylated sites (ie x[0]+y[0]=n). In fact, we can use either the starting condition that x[0]+y[0]=1 (so that x and y measure the proportion of each type of site) or x[0]+y[0]=n (so that x and y measure the number of each type of site) in the above equation.
Once we specify x[0] and y[0] and the parameters, the number of methylated sites can be determined at any time in the future.
Back to biology 301 home page.