Methylation Levels

Aim: To review the methods used for analysing one-variable dynamical models by examining how DNA methylation levels change over time.

In vertebrates, a very large proportion of CpG sites in the genome have methylated cytosines (75-85%).

Newly replicated DNA is unmethylated. Methylases recognize sites where the parental strand is methylated and the daughter strand is not and tend to methylate the daughter strand: maintenance methylation.

In addition to maintenance methylation, occasionally a site that was not previously methylated becomes methylated: de novo methylation.

Questions:

• How do methylation levels change over time?
• Do they reach a stable equilibrium level in the genome?
• If a large proportion of methyl groups are removed (e.g. by exposure to a cytosine analog, 5-azacytidine, that cannot be methylated), how long until the methylation levels approach equilibrium?

Model: Let

• p[t] equal the proportion of methylated CpGs at cell generation t
• q[t] equal the proportion of unmethylated CpGs at cell generation t (p[t]+q[t]=1)
• equal the proportion of methylated sites that remain methylated per cell division (maintenance methylation)
• equal the proportion of unmethylated sites that become methylated per cell division (de novo methylation)

Methylation Levels

From these definitions, we can find the proportion of methylated sites in the next cell generation:

p[t+1] = p[t] + (1 - p[t])

The proportion of unmethylated sites in the next cell generation would be:

q[t+1] = (1-) p[t] + (1-) (1 - p[t])

Check: Is p[t+1]+q[t+1] still equal to one?

Methylation Levels

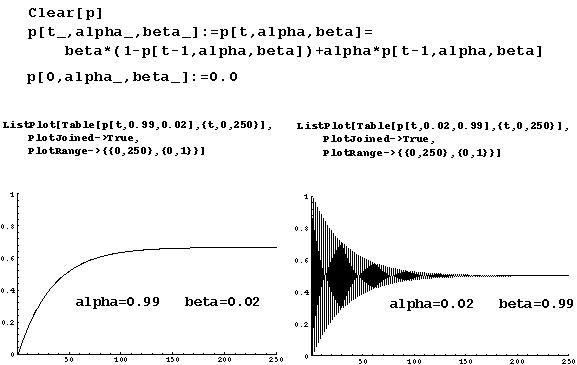
When p[t+1]=p[t], the system is at equilibrium. Let denote this value of p.

From the recursion, must solve

= + (1 - )

Putting the terms all on the same side:

(1- + ) =

The ONLY solution to this equation is

= /(1- + )

Let f(p) be given by the recursion:

f(p) = p + (1 - p)

f'(p) = d(f(p))/dp is:

f'(p) = -

Therefore f'() evaluated at is ( - ).

• 0 < f'() < 1 if > (locally stable equilibrium)
• -1 < f'() < 0 if < (locally stable with an oscillatory approach to equilibrium)

Methylation Levels

Empirical measurements indicate that maintenance methylation is about 10 to 100 times more common than de novo methylation.

Therefore, it is biologically reasonable to assume that is greater than , so that a smooth approach to equilibrium is predicted.

Finding the general solution is easier if we perform a transformation of variables.

With only one possible equilibrium, the best new variable to try is the difference between the current level of methylated CpG sites and the equilibrium level: x[t] = p[t]-.

The recursion then becomes

x[t+1] = p[t+1] - = p[t] + (1 - p[t]) -

x[t+1] = x[t] ( - )

This is much easier to iterate:

x[t] = x[t-1] ( - ) = x[t-2] ( - )²...

x[t] = x[0] ( - )^t

This is the general solution in terms of x[t]. In terms of p[t], we have:

p[t] = x[t] + = (p[0] - ) ( - )^t +

Methylation Levels

How do methylation levels change over time?

For biologically reasonable values of the parameters, methylation levels approach equilibrium in a smooth fashion.

Yes. The proportion of methylated sites at equilibrium is /(1- + ).

We can use the general solution,
p[t] = (p[0] - ) ( - )^t + ,
to find out how long it will take for methylation levels to be within 95% of equilibrium levels, given that the entire genome starts out unmethylated.
p[t] = 0.95 = (0 - ) ( - )^t +
Rearranging and solving for t gives: ( - )^t = 0.05
t= Log[0.05]/Log[ - ]

Methylation Levels

To proceed further, we must estimate the parameters.

In vertebrates, approximately 80% of CpG sites are methylated () and is approximately 50 .

This gives us two equations in two unknowns ( and ) which we can then solve for and :

= 50

0.8 = = /(1- + )

0.8 = /(1- 50 + )

0.8(1-49 ) =

= 0.0199 and =0.9950.

Therefore it takes approximately t = Log[0.05]/Log[0.9950 - 0.0199] = 118.8 cell generations for the genome to return to near equilibrium levels of methylation from a state in which no CpG sites are methylated.

Since it is estimated that 20-100 cell generations occur per individual generation for vertebrates, this indicates that methylation levels will return to near equilibrium within a few individual generations.

Back to biology 301 home page.